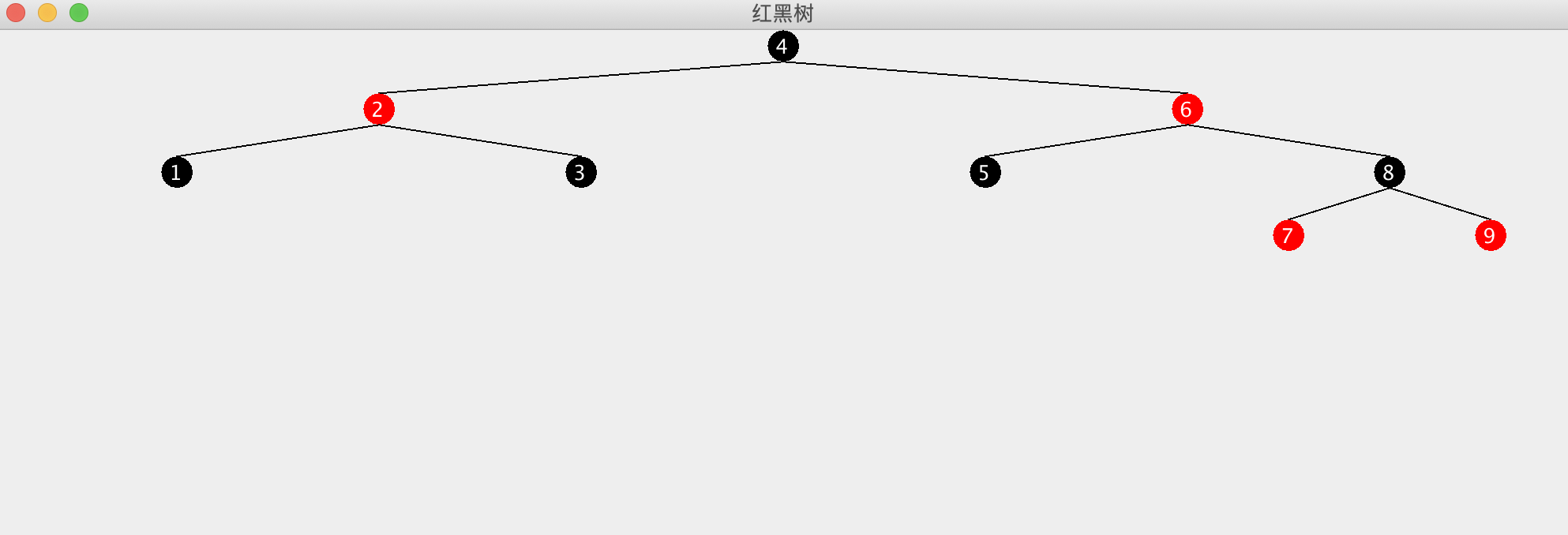
之前看 HashMap jdk1.8中的源码,就有提到红黑树,这次我们来了解以下红黑树究竟是怎样一种数据结构。
定义
红黑树(Red Black Tree)RBT 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
它是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的:它可以在O(log n)时间内做查找,插入和删除,这里的n是树中元素的数目。
二叉查找树
二叉查找树,Binary Search Tree 「BST」,我们首先看下二叉查找树有哪些特性呢?
- 某节点的左子树节点值仅包含小于该节点值
- 某节点的右子树节点值仅包含大于该节点值
- 左右子树每个也必须是二叉查找树
红黑树特征:
- 每个节点非黑即红
- 根节点是黑色的
- 每个叶节点都是黑色的
- 一个红色节点的直接子节点都是黑色的(不能有两个红色节点连着有父子关系)
- 从任意一个节点到叶节点,经过的黑色节点个数(黑高)是一样的
红黑树动态演示
这个网站可以帮助理解红黑树插入删除的过程。
变色的时机可能不太对,他统一放在最后变色了,理解上习惯右旋后直接变色,来判断下一步操作。
插入操作
插入会改变树的节点,树节点改变会有以下两种方式。
- 变色 recolor
- 旋转 rotation
为防止树全黑,且为了方便根节点到子节点黑色数相等,插入一般预设为红色节点
变色:
条件:父红叔红变颜色
颜色变化:父变黑,叔变黑,爷变红,如果变色不能达到红黑树的要求,再尝试旋转。
左旋
条件:父红叔黑右子树
右旋
条件:父红叔黑左子树
4种情况
- 父左子左
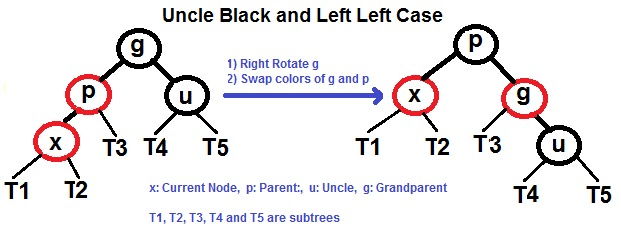
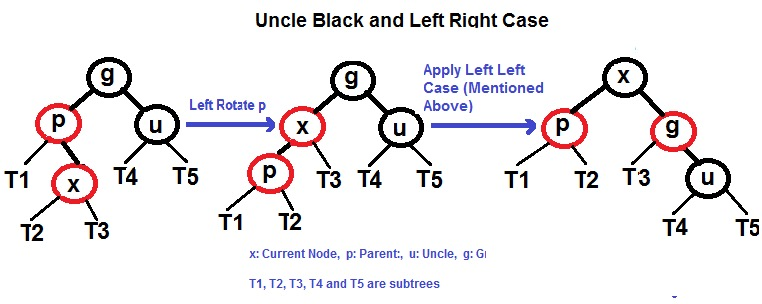
- 父左子右
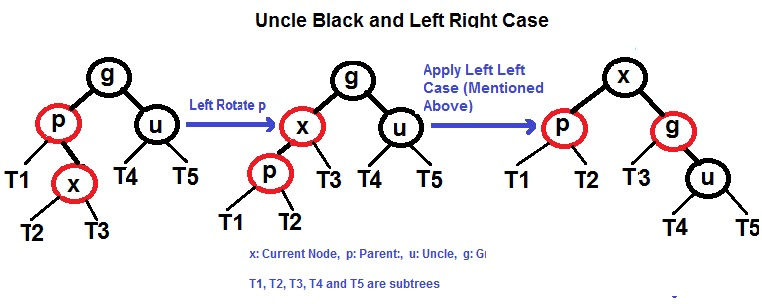
- 父右子右
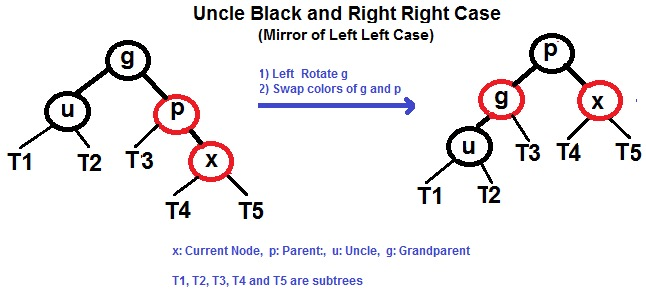
- 父右子左
删除操作
// todo 删除操作太麻烦了,先搁置
真佩服那些面试能手写红黑树的大佬,我能记个插入的几种情况就不错了,还得看着规则写。能写出删除操作的是真牛!!!小弟在此给大佬顶礼膜拜Orz。
手写红黑树代码
花了三天时间写出来的,估计挺多漏洞的,不过自己测了测插入目前没遇到啥问题,删除回头有空再写吧。算是自己造了个方形的轮子。
有点好处就是写了个toImage()方法,可以将构造的红黑树画出来,比较直观。下面上代码:
import javax.swing.*;
import java.awt.*;
/**
* @ClassName RedBlackTree
* @Description 红黑树
* @Author leo
* @Date 2019-09-24 09:57
**/
public class RedBlackTree extends JFrame {
static final int R = 0;//红色
static final int B = 1;//黑色
Node root;
public RedBlackTree() {
super();
initialize(500);// 调用初始化方法
}
static class Node {
//颜色
int color;
//值
int value;
//父节点
Node parent;
//左节点
Node left;
//右节点
Node right;
public Node(int value) {
this.color = R;
this.value = value;
}
}
/**
* 插入新节点 值为参数
*
* @param value
*/
public void insert(int value) {
Node newNode = new Node(value);
insert(newNode);
}
/**
* 插入新节点
*
* @param newNode
*/
public void insert(Node newNode) {
Node curNode = root;
if (root == null) {
root = newNode;
//判断是否符合规则
judgeRule(newNode);
} else if (curNode.value > newNode.value) {
if (curNode.left != null) {
insert(curNode.left, newNode);
} else {
curNode.left = newNode;
newNode.parent = curNode;
//判断是否符合规则
judgeRule(newNode);
}
} else {
if (curNode.right != null) {
insert(curNode.right, newNode);
} else {
curNode.right = newNode;
newNode.parent = curNode;
//判断是否符合规则
judgeRule(newNode);
}
}
}
/**
* 插入递归寻找合适位置
*
* @param curNode
* @param newNode
*/
public void insert(Node curNode, Node newNode) {
if (curNode.value > newNode.value) {
if (curNode.left != null) {
insert(curNode.left, newNode);
} else {
curNode.left = newNode;
newNode.parent = curNode;
//判断是否符合规则
judgeRule(newNode);
}
} else {
if (curNode.right != null) {
insert(curNode.right, newNode);
} else {
curNode.right = newNode;
newNode.parent = curNode;
//判断是否符合规则
judgeRule(newNode);
}
}
}
/**
* 判断是否符合规则
*
* @param curNode
*/
public void judgeRule(Node curNode) {
//判断是否父节点也是红色
if (curNode.parent == null) {
//父节点为空,说明节点是根节点,变黑色
curNode.color = B;
root = curNode;
} else {
//不是根节点
if (curNode.parent.color == R) {
//父节点也为红色
Node grandparent = curNode.parent.parent;
Node uncle;
int parentLR; //0左 1右
if (curNode.parent == grandparent.left) {
parentLR = 0;
//父亲左子树
if (grandparent.right != null) {
//不为null
uncle = grandparent.right;
} else {
//null节点 黑色
uncle = null;
}
} else {
parentLR = 1;
//父亲右子树
if (grandparent.left != null) {
//不为null
uncle = grandparent.left;
} else {
//null节点 黑色
uncle = null;
}
}
if (uncle != null && uncle.color == R) {
//父红叔红变颜色
recolor(curNode, uncle);
} else {
//父红叔黑判断 当前节点左右子树
if (curNode.value < curNode.parent.value) {
if (parentLR == 0) {
//父左子左 右旋
rightRotate(curNode.parent);
} else {
//父右子左 右旋
RLRotate(curNode);
leftRotate(curNode);
}
} else {
if (parentLR == 1) {
//父右子右 左旋
leftRotate(curNode.parent);
} else {
//父左子右 左旋
LRRotate(curNode);
rightRotate(curNode);
}
}
}
}
}
}
/**
* 变色
*
* @param curNode
* @param uncle
*/
private void recolor(Node curNode, Node uncle) {
//父变黑
curNode.parent.color = B;
//叔变黑
uncle.color = B;
//爷变红
uncle.parent.color = R;
judgeRule(uncle.parent);
}
/**
* 左旋 父子互换,前父挂左子,前子挂前爷,父子颜色互换
*
* @param curNode
*/
private void leftRotate(Node curNode) {
//当前父节点
Node parent = curNode.parent;
//当前爷节点
Node grandparent = curNode.parent.parent;
//判断爷节点是否为空
if (grandparent != null) {
//如果不为空
if (parent == grandparent.left) {
//父节点是左子树,当前节点就挂爷节点左子树
grandparent.left = curNode;
} else {
//父节点是右子树,当前节点就挂爷节点右子树
grandparent.right = curNode;
}
}
//当前父节点挂在当前节点左子树
parent.parent = curNode;
//当前节点左子树挂在前父节点右子树
parent.right = curNode.left;
if (parent.right != null) {
parent.right.parent = parent;
}
//当前节点左子树指向当前父节点
curNode.left = parent;
//当前节点挂到当前爷节点上
curNode.parent = grandparent;
//当前节点和当前父节点变色
int color = curNode.color;
curNode.color = parent.color;
parent.color = color;
if (curNode.parent == null) {
root = curNode;
}
}
/**
* 右旋 左子树
*/
private void rightRotate(Node curNode) {
//当前父节点
Node parent = curNode.parent;
//当前爷节点
Node grandparent = curNode.parent.parent;
if (grandparent != null) {
if (parent == grandparent.left) {
grandparent.left = curNode;
} else {
grandparent.right = curNode;
}
}
//当前父节点挂在当前节点左子树
parent.parent = curNode;
//当前节点右子树挂在前父节点左子树
parent.left = curNode.right;
if (parent.left != null) {
parent.left.parent = parent;
}
//当前节点左子树指向当前父节点
curNode.right = parent;
//当前节点挂到当前爷节点上
curNode.parent = grandparent;
//当前节点和当前父节点变色
int color = curNode.color;
curNode.color = parent.color;
parent.color = color;
if (curNode.parent == null) {
root = curNode;
}
}
/**
* 右左情况前置操作
*
* @param curNode
*/
private void RLRotate(Node curNode) {
//当前父节点
Node parent = curNode.parent;
//当前爷节点
Node grandparent = curNode.parent.parent;
//当前节点挂到爷节点上
curNode.parent = grandparent;
//爷节点的右子树指向当前节点
grandparent.right = curNode;
//前父节点挂当前节点
parent.parent = curNode;
//当前节点右子树
parent.left = curNode.right;
if (parent.left != null) {
parent.left.parent = parent;
}
//当前节点
curNode.right = parent;
}
/**
* 左右情况前置操作
*
* @param curNode
*/
private void LRRotate(Node curNode) {
//当前父节点
Node parent = curNode.parent;
//当前爷节点
Node grandparent = curNode.parent.parent;
//当前节点挂到爷节点上
curNode.parent = grandparent;
//爷节点的左子树指向当前节点
grandparent.left = curNode;
//前父节点挂当前节点
parent.parent = curNode;
//当前节点右子树挂前父节点左子树
parent.right = curNode.left;
if (parent.right != null) {
parent.right.parent = parent;
}
curNode.left = parent;
}
/**
* 画布初始化
*
* @param paperSize
*/
private void initialize(int paperSize) {// 初始化方法
this.setSize(paperSize * 2, paperSize);// 设置窗体大小
setDefaultCloseOperation(EXIT_ON_CLOSE);/// 设置窗体关闭方式
this.setTitle("绘制几何图形");// 设置窗体标题
MyCanvas c = new MyCanvas(paperSize);// 创建画布对象
add(c);// 将画布添加到窗体中
}
private class MyCanvas extends Canvas {// 创建内部类MyCanvas继承Canvas
//节点半径
int nodeRadius = 10;
//画布大小
int paperSize;
//层级限制
int levelLimit = 6;
//连线在x轴投影长度计算常量
int xLineLength = 512;
MyCanvas(int paperSize) {
this.paperSize = paperSize;
}
@Override
public void paint(Graphics g) {
Graphics2D g2 = (Graphics2D) g;// 调用新画图类Graphics2D(强制转化为Graphics2D这个类)
draw(g2, paperSize - nodeRadius, 0, root, 1);
}
private void draw(Graphics2D g2, int x, int y, Node node, int level) {
if (level > levelLimit) {
level = levelLimit;//设置大于level限制,线x轴长度就不变了,展示可能会重叠,画布越大这个层级可以越高
}
//设置节点颜色
g2.setColor(node.color == 1 ? Color.BLACK : Color.RED);
//画填充色圆
g2.fillOval(x, y, nodeRadius * 2, nodeRadius * 2);// 画一个圆形-坐标、宽高(Draw方法绘制的图形是空心的)
//设置值的颜色为白色
g2.setColor(Color.WHITE);
g2.drawString(String.valueOf(node.value), x + nodeRadius / 2, y + nodeRadius / 2 * 3);
//连线颜色为黑色
g2.setColor(Color.BLACK);
//线x轴投影长度
int lineX = xLineLength >> level++;
if (node.left != null) {
g2.drawLine(x + nodeRadius, y + nodeRadius * 2, x + nodeRadius - lineX, y + nodeRadius * 4);
draw(g2, x - lineX, y + nodeRadius * 4, node.left, level);
}
if (node.right != null) {
g2.drawLine(x + nodeRadius, y + nodeRadius * 2, x + nodeRadius + lineX, y + nodeRadius * 4);
draw(g2, x + lineX, y + nodeRadius * 4, node.right, level);
}
}
}
}
测试代码
public static void main(String[] args){
int[] arr = {1,2,3,4,5,6,7,8,9};
RedBlackTree rbt = new RedBlackTree();
for (int a:arr){
rbt.insert(a);
}
rbt.setVisible(true);
}
输出图像